由于Leetcode上关于层次遍历的题目比较多,所以单独一篇文章来讲解
# 1. 层次遍历相关的题目
102. 二叉树的层序遍历 - M (opens new window)
字节 - 18 , 微软 - 6
107. 二叉树的层序遍历 II - M (opens new window)
103. 二叉树的锯齿形层序遍历 - M (opens new window)
==高频==
637. 二叉树的层平均值- E (opens new window)
429. N 叉树的层序遍历 (opens new window)
微软 - 2
# 102. 二叉树的层序遍历 - M (opens new window)
字节 - 18 , 微软 - 6 , 亚马逊 - 13
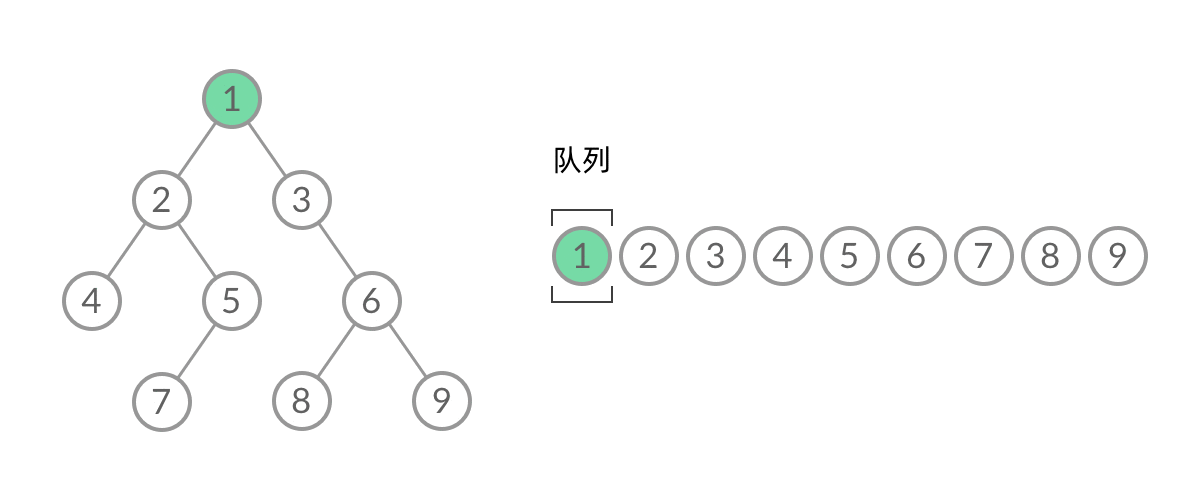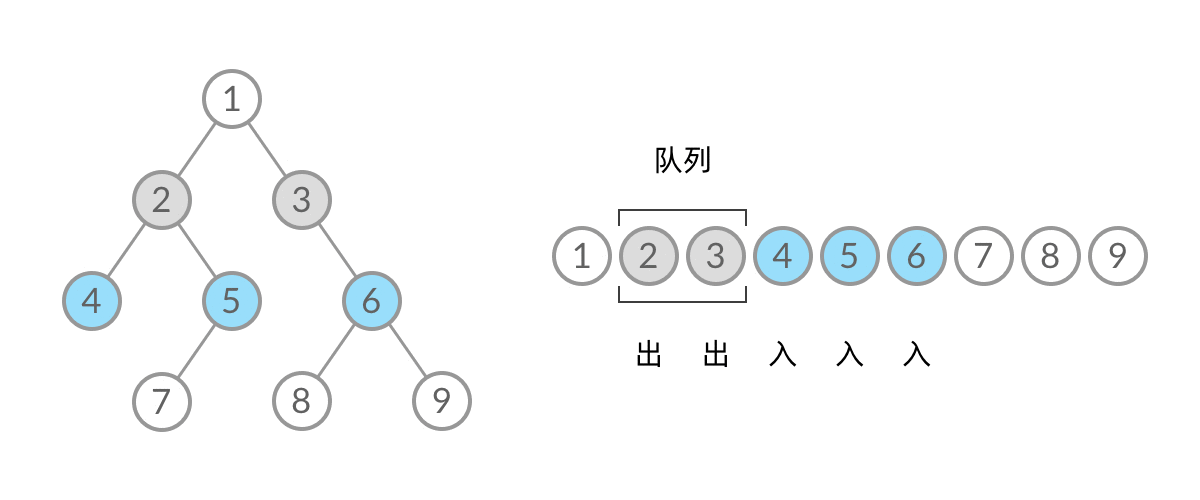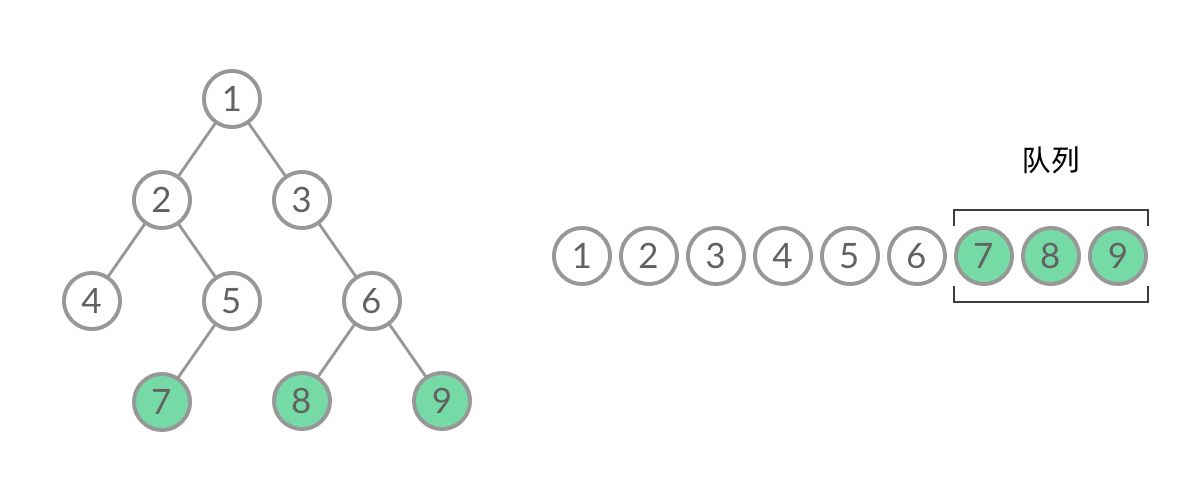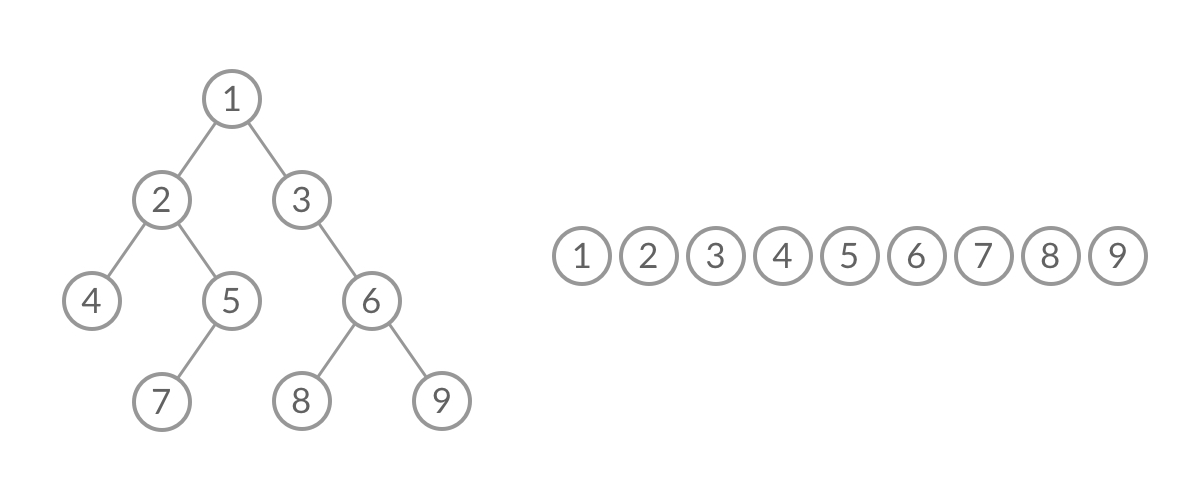
二叉树的层次遍历是必须要掌握的,需要用到队列
public class Solution{
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList();
if(root == null){
return result;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();
List<Integer> level = new ArrayList();
while(size -- > 0){
TreeNode node = queue.poll();
level.add(node.val);
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
result.add(level);
}
return result;
}
}
# 107. 二叉树的层序遍历 II - M (opens new window)
字节- 6 ,微软 - 2
这道题目与102 (opens new window)的差别在于:此题要求是 自底向上的层序遍历
我们采用头插法即可。
public class Solution{
public List<List<Integer>> levelOrderBottom(TreeNode root){
List<List<Integer>> result = new ArrayList();
if(root == null){
return result;
}
Queue<TreeNode> queue = new LinkedList();
queue.add(root);
while(!queue.isEmpty()){
int size = queue.size();
List<Integer> level = new ArrayList();
while(size-- > 0){
TreeNode node = queue.poll();
level.add(node.val);
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
// 头插法
result.add(0,level);
}
return result;
}
}
# 103. 二叉树的锯齿形层序遍历 - M (opens new window)
字节 - 18 , 微软 - 14 ,亚马逊 - 22
此题是Z字形的层次遍历
public class Solution{
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList();
if(root == null){
return root;
}
Queue<TreeNode> queue = new LinkedList();
queue.offer(root);
boolean isReversed = false;
while(!queue.isEmpty()){
int size = queue.size();
List<Integer> level = new ArrayList();
while(size-- > 0){
TreeNode node = queue.poll();
// 处理 Z字形的关键
if(isReversed){
level.add(0,node.val);
}else{
level.add(node.val);
}
if(root.left != null){
queue.offer(node.left);
}
if(root.right != null){
queue.offer(node.right);
}
}
result.add(level);
isReversed = !isReversed;
}
return result;
}
}
# 637. 二叉树的层平均值- E (opens new window)
public class Solution{
public List<Double> averageOfLevels(TreeNode root) {
List<Double> result = new ArrayList();
if(root == null){
return result;
}
Queue<TreeNode> queue = new LinkedList();
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();
double sum = 0.0;
// 注意这里采用for循环是一个小技巧,
for(int i = 0 ;i < size; i ++){
TreeNode node = queue.poll();
sum += node.val;
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
result.add(sum/size);
}
return result;
}
}
# 429. N 叉树的层序遍历 (opens new window)
微软 - 2
N叉树相较于二叉树,子树多了而已。但是其遍历的思路是不变的。
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> result = new ArrayList();
if(root == null){
return result;
}
Queue<TreeNode> queue = new LinkedList();
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();
List<Integer> level = new ArrayList();
while(size-- > 0){
TreeNode node = queue.poll();
level.add(node.val);
// 相较于二叉树,只有这里判断子树的数量不同
for(TreeNode tmp:node.children){
queue.offer(tmp);
}
}
result.add(level);
}
return result;
}
}
# 2.利用层次遍历的性质的题目
111. 二叉树的最小深度 (opens new window)
993. 二叉树的堂兄弟节点 (opens new window)
微软- 4,亚马逊 -4
# 993. 二叉树的堂兄弟节点 (opens new window)
微软- 4,亚马逊 -4
解题思路:使用层序遍历,如果两个结点在同一层,它们就是堂兄弟结点(排除一种情况,那就是“这两个结点的父亲结点相同”)
public class Solution {
public boolean isCousins(TreeNode root, int x, int y) {
// 这两个值任意一个都不会出现在根节点
if(root == null || root.val == x || root.val == y){
return false;
}
Queue<TreeNode> queue = new LinkedList();
queue.offer(root);
// 定义2个节点
TreeNode xNode,yNode;
// 为了判断其父节点是否相同,还需要定义出其父节点
TreeNode xParent,yParent;
while(!queue.isEmpty()){
int size = queue.size();
while(size -- > 0){
TreeNode node = queue.poll();
if(node.left != null){
queue.offer(node.left);
if(node.left.val == x){
xNode = node.left;
xParent = node;
}
if(node.right.val == y){
yNode = node.right;
yParent = node;
}
}
if(node.right != null){
queue.offer(node.right);
if(node.right.val == x){
xNode = node.right;
xParent = node;
}
if(node.right.val == y){
yNode = node.right;
yParent = node;
}
}
}
/** 这里要处理的逻辑
* 某一层俩节点都为空,说明不在这一层;
* 同一层的xNode和yNode有一个为空,则直接返回false;
* 两个都不为空时,需要判断其父节点是否相同。
*/
if(xNode == null && yNode == null){
// 说明x,y都不在这层,不用处理
}else if(xNode != null && yNode != null){
// 如果父亲结点不相等,说明是堂兄弟结点
return xParent == yParent;
}else{
// 这里的size == 0表示这一次遍历完毕,只存在xNode或者yNode
if(size == 0){
return false;
}
}
}
return false;
}
}
# 111. 二叉树的最小深度 (opens new window)
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
public class Solution {
public int minDepth(TreeNode root){
if(root == null) return 0;
if(root.left != null && root.right == null){
return minDepth(root.left) + 1;
}
if(root.left == null && root.right != null){
return minDepth(root.right) + 1;
}
return Math.min(minDepth(root.left),minDepth(root.right))+1;
}
广度优先搜索的性质保证了最先搜索到的叶子节点的深度一定最小,当我们找到一个叶子节点时,直接返回这个叶子节点的深度。
public class Solution {
public int minDepth(TreeNode root){
if(root == null){
return 0;
}
int depth = 1;
Queue<TreeNode> queue = new LinkedList();
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();
while(size -- >0){
TreeNode node = queue.poll();
// 广度优先搜索(层次遍历)的性质保证了最先搜索到的叶子节点的深度一定最小。
if(node.left == null && node.right == null){
return depth;
}
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
depth += 1;
}
return depth;
}
# 314. 二叉树的垂直遍历 (opens new window)
微软 -3 , 亚马逊 - 5
此题留待日后再解...